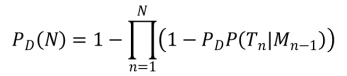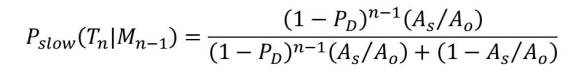Recently, I analyzed a surveillance problem for a C3ISR company and applied analysis from O. Donn Grace’s Sonar and Anti-Submarine Warfare, Chapter 14, Operational Performance. The analysis directly applies to active (sonar or radar) search but I applied it to the passive case using Washburn’s integral technique.
The probability of declaration (detection, classification, etc.) after N tries is:
where PD is the probability of declaration of a target in an interrogation cell due to signal and/or data processing in that cell. This probability is held to be constant over the search area (i.e., a ‘mean value’ approximation). The probability P(Tn|Mn-1) is the measure that the target is declared in some search cell within a surveillance or operational area on the nth trial given that it was missed in all prior trials. This result is due to a Bayesian relationship developed in the text.
If a target moves quickly in the surveillance field such that each search area is non-overlapping then
where As is the illuminated (or ensonified) search area (within which the declaration cells lie) and Ao is the operational area.
If a target moves slowly (i.e., is fixed) in the search area then each scan is correlated to the next (overlapping areas) and
where this equation is derived from Bayes theorem and the chain rule. Both the fast and slow probabilities are equal on the first scan. The slow probability is asymptotic to zero on further scans whereas the fast probability remains constant scan to scan or interrogation to interrogation.
The cumulative probability for fast or slow targets with, for example, PD = 0.5 and As/Ao = 0.3 are plotted versus scan number in this figure:
 The operational area may be subdivided to increase the search to operational area ratio at the expense of more search sensors.
The operational area may be subdivided to increase the search to operational area ratio at the expense of more search sensors.